Zapata de medianería con viga centradora.

La solución de la zapata de medianería por medio de la viga centradora, consiste en recurrir a la colaboración del pilar y zapata próxima para, por medio de una viga de unión, crear un mecanismo que centre la carga de la zapata de medianería.

Si N1 y N2 son las cargas verticales que transmiten los pilares 1 y 2 (fig. 3.33) por medio de la viga centradora se establece un par que centra la carga de la zapata correspondiente al pilar 1. 

 Figura 3.33 

Según los esquemas de la figura 3.34  se establece el equilibrio de fuerzas y momentos.

 Figura 3.34

 

De tas expresiones (1) y (2) se deduce que la reacción correspondiente al pilar 1, ha aumentado respecto a la que tendría como zapata aislada, y, por el contrario, ¡a reacción correspondiente al pilar 2 ha disminuido.
Conforme con este planteamiento, el procedimiento de cálculo es el siguiente:
 

1. Predimensionar las zapatas 1 y 2 como si las cargas N1 y N2 fuesen centradas, mayorándolas en un 40% lo aproximadamente la 1 y en un 10% la 2, para tener en cuenta el peso de las zapatas y el incremento en la reacción  R1. 

 

2. Conocida la dimensión a’1, y siendo a1 el canto del pilar 1, se calcula la excentricidad e:

 

3. Los valores de las reacciones serán:

 

4. Las tensiones del terreno bajo cada una de las zapatas serán:

 

En caso de no ser u1 y/o u2 menor que la u, dm. se corrigen los cálculos desde el punto 2, aumentando las dimensiones necesarias.
 

5. Los momentos y cortantes en el conjunto siendo: 

 

Se calculan como viga isostática.

Para el calculo de la viga centradora se calculan los cortantes V1 = V2 y los momentos flectores M1 y M2 figura 3.35

 Figura 3.35

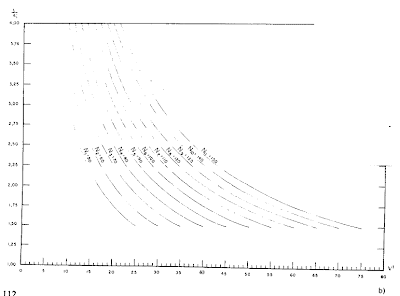
Los ábacos de las figuras 3.36 a) y b) dan directamente los valores de servicio

 en función de la relación

 , para distintos valores de la carga N1.

Si en los pilares, además de la carga vertical N1 y N2, existiesen momentos, el planteamiento es similar, sumando algebraicamente los momentos existentes al establecer el equilibrio de momentos. 

 Figura 3.36