1. Análisis mecánico por hidrómetro.
Aunque existen tamices con aberturas de malla menores a 0.075 mm, no es apropiado su uso para determinar la distribución del tamaño de partículas de la fracción de suelo fino, debido a que las partículas del suelo fino no siempre tienen textura granular sino en hojuelas y estas últimas poseen propiedades eléctricas importantes que dificultarían el tamizado.
Stokes (1850) desarrolló una ecuación que relaciona la velocidad de descenso de una partícula esférica en un fluido con respecto al tamaño de esta, que es:
Donde:
v = Velocidad de descenso de la partícula.
gs = Peso unitario de los sólidos del suelo
gw = Peso unitario del agua.
h = Viscosidad dinámica del fluido.
D = Diámetro de la partícula con forma esférica.
Con el concepto que encierra la ecuación [1.43] conocida también como la ley de Stokes, puede determinarse el tamaño del más del 90% de las partículas del suelo fino. El hidrómetro del tipo ASTM 152H que se muestra en la Figura 1.23a, es un instrumento de laboratorio para medir la gravedad específica de un líquido (Figura 1.23b).
El análisis mecánico por hidrómetro está basado en el principio de sedimentación de las partículas del suelo fino en suspensión. Cuando un suelo fino es dispersado en agua, las partículas sedimentarán a diferentes velocidades, dependiendo de su textura, tamaño y masa, además de la viscosidad del agua. Para simplificar el análisis, se asume que las partículas tienen forma esférica de tal manera que puede utilizarse la ley de Stokes para describir su comportamiento. El diámetro de la partícula según la ecuación [1.43] será:
La velocidad v de está ecuación puede escribirse como:
Donde:
L = Es la distancia que recorre la partícula al sedimentarse.
t = Es el tiempo que tarda en recorrer esa distancia.
Reemplazando:
en esta ecuación y factorizando se tendrá que:
Donde: Gs = Gravedad específica del suelo fino.
Figura 1.23. Hidrómetro (Das, 1998).
(a) Hidrómetro tipo ASTM 152H. (b) Determinación de la gravedad específica.
Debe tenerse cuidado al manejar las unidades de los diferentes valores que incluye esta ecuación. El diámetro de la partícula por ser un valor pequeño conviene manejarlo en mm, la viscosidad del agua se mide en g·s/cm2, el peso unitario del agua en g/cm3, la distancia L que recorre la partícula conviene medirla en cm y el tiempo de la sedimentación es muy lento por lo que debe medirse en minutos. Compatibilizando unidades se tendrá que:
Por lo que se tendrá que:
Sin embargo, para determinar fácilmente del diámetro de la partícula, la ecuación [1.43] puede escribirse:
Donde:
Tanto la gravedad específica como la viscosidad del agua dependen de la temperatura, por lo cual la norma ASTM D422 ha tabulado valores para el coeficiente K en función a la temperatura y la gravedad específica, que se muestran en la Tabla 1.9.
Tabla 1.9. Valores de K (ASTM D422).
En laboratorio el análisis mecánico por hidrómetro, se realiza en un cilindro (18” x 2.5”) con agua mantenida a temperatura constante donde es introducida una cantidad apropiada de suelo. Para dispersar las partículas en todo el fluido y acelerar la sedimentación, se introduce defloculador que por lo general es hexametafosfato de sodio. La solución debe ser mezclada enérgicamente para homogenizar el fluido, es recomendable que la cantidad total de fluido sea de 1000 ml, por lo que talvez deba añadirse agua destilada.
Cuando el hidrómetro es colocado en el cilindro (Figura 1.23b) este queda suspendido a cierta profundidad, a medida que las partículas en suspensión sedimenten el hidrómetro se hundirá consecuentemente, ya que la gravedad específica del fluido está en función al contenido de partículas por unidad de volumen en suspensión. La lectura del hidrómetro se realiza del punto que esta en el centro del bulbo del hidrómetro hasta la medida que marca el nivel superior de agua en la regla graduada, esta distancia es L en la Figura 1.23b. Este valor puede obtenerse de la siguiente expresión:
Donde:
L = Profundidad sumergida del bulbo del hidrómetro.
L1 = Medida de la profundidad sumergida de la parte superior del bulbo.
L2 = Longitud del bulbo (14 cm para hidrómetro ASTM 152H).
VB = Volumen del bulbo del hidrómetro (67 cm3 para hidrómetro ASTM 152H).
A = Área de la sección transversal del cilindro (27.8 cm2 si es de 18” x 2.5”).
Tabla 1.10. Valores de L para distintas lecturas (R) del hidrómetro.
Para un hidrómetro del tipo ASTM 152H y un cilindro de sedimentación de 18” x 2.5”, se tendrá que:
L = L1 + 5.8
Para obtener el valor de L1 no se toma en cuenta el menisco que se forma entre la superficie del agua y el hidrómetro, por lo que la lectura L1 corregida del menisco será: R. Midiendo el valor de R en la regla graduada se determina la longitud L, que es el valor de la longitud en la ecuación [1.43]. La norma ASTM D422 presenta valores tabulados para la variación de L respecto a R válidos para el equipo de laboratorio anteriormente descrito, que se muestran en la Tabla 1.10.
Se toman lecturas con el hidrómetro de la densidad del fluido para diferentes intervalos de tiempo, que por lo general son:
t1 =15 seg, t2 =30 seg, t3=1 min, t4 = 2 min, t5 = 4 min,... ,t14=24 horas y t15 = 48 horas.
Con los valores de L y t para los diferentes intervalos de tiempo en la ecuación [1.44], se obtienen los diversos tamaños de partículas del suelo fino.
Con los valores de L y t para los diferentes intervalos de tiempo en la ecuación [1.44], se obtienen los diversos tamaños de partículas del suelo fino.
Curva de distribución del tamaño de partículas.
Al igual que el análisis mecánico por tamices se puede trazar la curva de distribución del tamaño de partículas para el suelo fino. Con la ecuación [1.44] se determina el tamaño de las partículas del suelo, pero el porcentaje de estas que pasan un tamaño de aberturas de un tamiz imaginario se puede determinar con la ecuación:
[1.45]
Donde el valor de a es una corrección para la gravedad específica, que será:
[1.46]
Este valor de corrección también puede ser obtenido de la Tabla 1.11
Es muy importante que la temperatura se mantenga constante durante todo el ensayo, para lograr esto en la práctica se sumerge el cilindro de sedimentación en un baño maría que mantiene el agua a temperatura constante. Sin embargo también deben aplicarse factores de corrección por temperatura y viscosidad del fluido al valor de R en la ecuación [1.45], donde la forma de aplicar todos estos se describe ampliamente en un manual especializado de laboratorio.
Todos los resultados son registrados ordenadamente en una tabla al igual que en el caso del suelo de grano grueso. Con los valores del tamaño de partículas en milímetros obtenidos de la ecuación [1.44], ubicados en orden inverso en el eje de las abscisas en escala logarítmica y el porcentaje de las partículas que pasan un tamiz imaginario obtenido de la ecuación [1.45], ubicada en el eje de las ordenadas, se traza la curva de distribución del tamaño de partículas como se observa en la Figura 1.24. Esta curva es la continuación de la curva de distribución del tamaño de partículas del suelo de grano grueso. En el sector donde se conectan estas dos curvas existe una ligera discontinuidad que por lo general se debe a las diferentes texturas de las partículas, esta debe corregirse manualmente para mantener la continuidad de las dos curvas, como se muestra en las curvas de la Figura 1.22b, d y e.
Figura 1.24. Curva de distribución del tamaño de partículas.

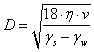


















No hay comentarios:
Publicar un comentario